Bonus Poker Vs Jacks Or Better
Triple Bonus Poker is a variation of Bonus Poker. That, in turn, is a
variation of Jacks or Better, the most basic form of video poker in the
business.
As a game, Bonus Poker actually represents a variation of Jacks or Better.It features a deck of 52 cards, while the lowest rank for a winning combination is a pair of Jacks. The return for a Full House or for a Flush, however, is lower compared to that, offered by 9/6 Jacks or Better. One advantage of playing Bonus Poker Deluxe, however, is the strategy is just as simple as Jacks or Better. There is no requirement to distinguish between four aces and four 2s, 3s or 4s or to distinguish between four aces and four 5s through Kings. All four of a kind hands are equal, just as they are in Jacks. 'Bonus Poker' by IGT) is a better game than 99.54% 9/6 Jacks. In 9/6 Jacks, for instance, 'QJ8', 'KQ9' and 'KJ9' are preferred to AKQJ. These are all 3-card straight flushes with two high cards and two gaps. In 8/5 Jacks (whether the quads return 25 or 35), 'QJ8' is preferred to AKQJ, but 'KQ9' and 'KJ9' are not. Jacks or Better is the least volatile out of all video poker variants, meaning the wins are modest and steady. Conservative video poker players enjoy this variant over the flashier and more volatile machines, such as Double Double Bonus Poker, because the risk is low and the payouts are fairly consistent.
This page compares Triple Bonus Poker to its antecedent games (Jacks or
Better, Bonus Poker, and Double Bonus Poker). We pay close attention to the pay
tables available, the resulting payback percentages, and what effects these
changes have on strategy for the game. We also include observations about where
to find Triple Bonus Poker online.
In Bonus Poker, you get bigger payouts for 4 of a kind hands. In Triple Bonus
Poker, these payouts are increased even further. They’re based on the rankings
of the cards in the hands, which are grouped as follows:
- Aces
- 2s, 3s, or 4s
- 5s through kings
The Basics for How to Play Triple Bonus
We cover the basics of video poker in general in this section, as well as how
they apply to Triple Bonus Poker.
Video poker games resemble slot machines, but the differences are major. Both
games require you to insert money. Both games involve a random number generator
assigning symbols to certain spots on a computer screen. And both games offer
payouts based on combinations of symbols on your screen.
The difference is that video poker uses recognizable and known
symbols-playing cards. This creates familiarity for the player, but more
importantly, it creates a math problem that can be solved.
A player has no way of knowing what the probability of getting a cherry or a
bar symbol on a slot machine. The numbers are set up arbitrarily. In fact, 2
identical slot machines might offer different probabilities even if they’re
sitting right next to each other on the casino floor.
But the numbers in the random number generator on a video poker game emulate
the probability you’d see if you were using a real deck of cards.
Any specific card has a 1/52 probability of coming up. A card of a specific
ranking comes up 1/13 of the time. A card of a specific suit comes up 1/4 of the
time.
To calculate the payback percentage for a gambling machine, you need 2 pieces
of data:

- The payoffs for the possible combinations
- The probability of getting those combinations
Slot machine designers and casino managers have those details for the slot
machine games on the casino floor, but the players don’t. The players only have
the payoffs, not the probability.
But in video poker, you have both pieces of information-the payoffs and the
probabilities.
This enables you to compare a specific pay table on a game like Triple Bonus
Poker with the pay table for another game to determine which one offers you the
better odds.
You could do the calculations with a pencil and paper, but it would take
forever. It’s also unnecessary, as multiple VP experts have already done the
calculations using computers.
We’ll go into more detail about how payback percentages work and are
calculated in the section devoted to that. For now, let’s talk about how the
actual gameplay works on a Triple Bonus Poker.
The first thing you’ll do when playing Triple Bonus Poker is insert money
into the machine. Triple Bonus and other video poker games are designated with a
denomination-like 25 cents, a dollar, or $5. When you input money, it’s
converted into credits based on that denomination.
You insert $200 into a $5 Triple Bonus game. You now have 40 credits (or
“coins”) to play with.
The bets and payoffs are all done in “coins” or “credits”. In this example,
each of those coins is worth $5.
To start playing, you decide how many coins you’re going to bet. In Triple
Bonus, you can bet 1, 2, 3, 4, or 5 coins.
But you should always bet 5 coins (“max bet”).
Here’s Why:
The top hand in Triple Bonus and most other video poker games is a royal
flush. That hands pays off at 200 for 1, but if you bet 5 coins, it pays off at
800 for 1.
That’s a huge difference. You’d feel like a fool if you bet 4 coins and got
dealt a royal flush.
Once you’ve placed your bet, the computer “deals” you a 5-card poker hand.
You then have the option to keep or discard any, none, or all the cards on the
screen. You do this by pressing the “hold” button on the machine below each card
you want to keep. On newer machines, you can just touch the card on the screen.
When you’ve finished making your decisions, you press the “draw” button to
get replacement cards. The computer randomly assigns you new cards in exchange
for the cards you discarded.
The game then compares you final hand to the pay table and pays you off based
on the poker hand value of your final hand.
You’ll notice that you’re making decisions during this game that can affect
your outcome. The absurd but obvious example is someone who discards any cards
if she’s dealt a royal flush. She’d be giving up the top-paying hand in the game
to speculate on what would certainly be a lower-paying hand.
These decision points are why video poker is a skill-based game. We’ll
discuss strategy decisions for Triple Bonus in a designated section later on
this page.
For now, let’s look at how the pay tables work in Triple Bonus.
Triple Bonus Pay Tables, Payback Percentages, and the House
The Triple Bonus pay table is just a list of poker hands with the payouts
for each of those hands. We’ll post an example below, then we’ll discuss what
some of those numbers mean afterward:
| Hand/Coins | 1 coin | 2 coins | 3 coins | 4 coins | 5 coins |
|---|---|---|---|---|---|
| Royal flush | 200 | 400 | 600 | 800 | 4000 |
| Straight flush | 50 | 100 | 150 | 200 | 250 |
| 4 of a kind – aces | 240 | 480 | 720 | 960 | 1200 |
| 4 of a kind – 2s, 3s, or 4s | 120 | 240 | 360 | 480 | 600 |
| 4 of a kind – 5s through kings | 75 | 150 | 225 | 300 | 375 |
| Full house | 10 | 20 | 30 | 40 | 50 |
| Flush | 7 | 14 | 21 | 28 | 35 |
| Straight | 5 | 10 | 15 | 20 | 25 |
| 3 of a kind | 3 | 6 | 9 | 12 | 15 |
| 2 pairs | 1 | 2 | 3 | 4 | 5 |
| Pair of kings or better | 1 | 2 | 3 | 4 | 5 |

The first thing to notice is the increased payout for the royal flush. We
talked about that before, but it bears repeating:
Always bet 5 coins so that you can get the big jackpot if you hit a royal
flush.
The next thing to notice is the payoffs for the 4 of a kind hands. Other
video poker games just pay off based on the final value of the hand without
making a distinction based on ranking.
But Bonus Poker games like Triple Bonus offer bigger payoffs based on the
rank of the cards in the hand. The aces are the best possible 4 of a kind in
this game, with 2s, 3s, or 4s being the next best. The other hands, 5s through
kings, all offer a lower payoff.
The standard version of video poker is Jacks or Better, and the payoff for
any 4 of a kind in that game is 25 for 1.
Even the worst possible 4 of a kind in Triple Bonus pays 3 times that much-75
coins. This is how the game gets its name, in fact.
By the way, if you guessed based on what we’ve discussed so far that the
payoffs in Double Bonus Poker for a 4 of a kind start at 50 for 1, give yourself
a gold star.
Remember, too, when we talked about how you can use this information to get
an overall payback percentage for the game?
Let’s talk about what that means now.
The payback percentage is the long-term expected return to the player for the
game. It’s how much of each bet the video poker designer and casino managers
expect to pay out in winnings.
an average of $99 in winnings for every $100 bet, making an average $1 profit.
This is, of course, an average over thousands of spins. It’s impossible to
get results like this in the short run, in fact. On a single video poker hand,
you’ll lose $1 or win at least $1. There is no “win 99 cents” result possible.
But if you play 2 video poker hands, losing $1 on one hand and winning $3 on
the other, you’re up $2. Based on that tiny sample size, the game would seem to
have a positive expectation.
For the casinos (and to an extent, for the players), this is a feature, not a
bug. If short-term probability on these games didn’t work this way, no one would
ever walk away a winner. And no one would ever play.
The calculations for these expected returns are reasonably easy to make, too.
You simply multiply the payoff for each possibility by the probability of
getting that result.
The probability of getting a pair of kings or better in this game is 10.8%.
Since the payoff for this hand is 1 unit, this adds 10.8% to the overall payback
percentage for the game.
The probability of getting 2 pairs in this game is 11.8%. This hand also pays
off at 1 for 1, so this adds another 11.8% to the overall payback percentage for
the game.
The probability of getting 3 of a kind is 7.3%. Since this hand pays off at 3
for 1, we multiply 7.3% by 3 to get another 21.9% added to the payback
percentage for the game.
We can continue with every hand in the game, and when we add them all up, we
get the overall payback percentage for the game. With the pay table listed
above, the payback percentage for Triple Bonus Poker is 99.94%.
This number assumes you’re playing every hand with optimal strategy, by the
way. We’ll talk more about that in the next section, but right now, we’d like to
make a couple more observations about the pay table.
You’ll notice the payoffs on this game start with a pair of kings or better.
This is one of the ways the game can afford to offer the much higher payouts for
the 4 of a kind hands. Most video poker games pay off for a pair of jacks or
better. By paying off only on kings or aces, the game has halved the number of
winning possibilities for that hand.
Most games pay off 2 for 1 on 2 pairs, too. The payout is reduced in Triple
Bonus to even money again.
The overall effect of these changes with the above table is a higher average
expected return, but it’s also a higher volatility game.
What does volatility mean?
It’s a measure of how wild the swings in your bankroll are as you get into
the long run and start moving toward the expected return.
Since the hands that have the most common payoffs come up less often, you’ll
probably see longer losing streaks and a dwindling bankroll as you shoot for
those 4 of a kind hands. When you do hit a 4 of a kind, you’ll start to “catch
up”.
You’ll notice this on all variation of Bonus Poker, by the way-not just
Triple Bonus. Every time you get a bigger payout for a hand like 4 of a kind,
one of the more common hands has a lower payout.
But let’s get back to that 99.94% number.
What does that mean over the long run?
An average video poker player makes 600 spins per hour. If you’re playing for
$25 per spin (5 coins on a $5 machine), you’re putting $15,000 per hour into
action. Your expected return is $14,991 per hour, so your net hourly loss is
only $9 per hour on this game.
For a game with those kinds of stakes, that’s a minimal amount to lose.
But not all Triple Bonus Poker games offer that pay table.
Here’s a more common Triple Bonus pay table:
| Hand/Coins | 1 coin | 2 coins | 3 coins | 4 coins | 5 coins |
|---|---|---|---|---|---|
| Royal flush | 200 | 400 | 600 | 800 | 4000 |
| Straight flush | 50 | 100 | 150 | 200 | 250 |
| 4 of a kind – aces | 240 | 480 | 720 | 960 | 1200 |
| 4 of a kind – 2s, 3s, or 4s | 120 | 240 | 360 | 480 | 600 |
| 4 of a kind – 5s through kings | 75 | 150 | 225 | 300 | 375 |
| Full house | 10 | 20 | 30 | 40 | 50 |
| Flush | 7 | 14 | 21 | 28 | 35 |
| Straight | 4 | 8 | 12 | 16 | 20 |
| 3 of a kind | 3 | 6 | 9 | 12 | 15 |
| 2 pairs | 1 | 2 | 3 | 4 | 5 |
| Pair of kings or better | 1 | 2 | 3 | 4 | 5 |
The only difference between this pay table and the previous one is the payoff
for a straight. (We italicized that line to highlight the difference.) Instead
of getting 5 for 1 on a straight, you’re now getting 4 for 1.
This reduces the payback percentage from 99.94% to 99.59%.
That same player from earlier is now looking at an hourly expected return of
$14,938.50, which equates to an hourly loss of $62.50.
There’s a big difference between losing $9/hour and losing $62.50/hour.
And that’s just the difference caused by reducing the payoff on a straight.
Video poker experts and authors use a kind of short hand to describe these
pay tables, by the way. That first pay table is a 10/7/5 Triple Bonus game. The
second pay table is a 10/7/4 Triple Bonus Game.
The numbers represent the payoffs for the full house, flush, and straight,
respectively.
There are also Triple Bonus Poker pay tables that look like this and have the
following payback percentages:
- 9/7/4 Triple Bonus – 97.45%
- 9/6/4 Triple Bonus – 95.88%
- 9/5/4 Triple Bonus – 94.53%
You’ll notice that when the game starts reducing the payoff for the full
house, the payback percentage takes a huge nosedive.
If you’ve read our other video poker pages, you’ll know that we recommend
sticking with VP games with a 99% payback percentage or higher. Two of the pay
tables for Triple Bonus qualify, but the other 3 do not. Skip those 3 pay tables
in the bulleted list above.
Triple Bonus Poker Strategy
Of course, those expected returns and payback percentages assume you’re
making the mathematically optimal decision on every hand. To do that, you need
to know when to hold em and know when to fold em. (Sorry, Kenny Rogers-I
couldn’t resist.)
A video poker strategy chart can be compared to a basic strategy chart in
blackjack. Some decisions offer a better expected return than others. By
sticking to the strategy chart, you can rest assured that your decisions are
close to mathematically optimal.
Here’s an example of a video poker decision and why one choice might be more
optimal than another:
Suppose you’re dealt a 5-card hand consisting of the jack, queen, king, and
ace of hearts. The 5th card is the king of diamonds.
You have a draw to a royal flush, which pays off at 800 for 1. You also have
a sure thing-a pair of kings, which pays off at even money.
One option offers you a roughly 2% chance of upgrading to an 800 for 1
payoff. That’s an expected value of 16.
The other offers a 100% chance of getting even money. That’s an expected
value of 1. You also have a remote probability of upgrading to 3 of a kind, but
that probability is only about 1%. 1% of a 3 for 1 payoff doesn’t add much to
your expected return. You have a minimal chance of getting 2 kings, and the
payoff for that is a respectable 75 for 1, but the probability is far less than
1%.
Even with all the other possibilities, the payoff for the royal flush makes
the draw to the royal flush the clearly obvious choice.
What a video poker strategy chart does is provide a ranked list of hands. You
start at the top, comparing those hands to what you’re holding. When you get to
a hand that matches what you have, you keep those cards and discard the others.
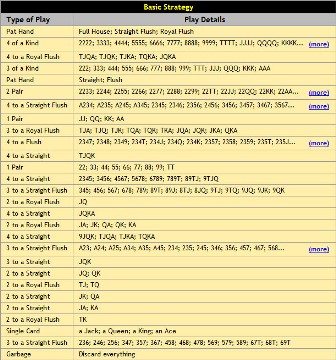
Here’s a simplified Triple Bonus strategy chart for your use:
- Royal flush, straight flush, any 4 of a kind
- 4 cards to a royal flush
- Full house, flush, straight, 3 of a kind
- 3 cards to a straight flush
- 2 pair (Just keep the high pair)
- High pair (aces or kings)
- 3 cards to a royal flush
- 4 cards to a flush
- Unsuited K Q J T
- Low pair (jacks to 2s)
- 4 cards to an outside straight
- 3 cards to a straight flush
- Unsuited A K Q J
- 4 cards to an inside straight w / 3 high cards
- Unsuited K Q J
- Unsuited Q J
- Unsuited K Q, K J
- Suited J 10
- Unsuited A K, A Q, A J
- Ace
- Suited K T, Q T
- King, queen, or jack
- Discard everything
Here are some observations that might help you understand the strategy as
described:
If you get a royal flush, a straight flush, or a 4 of a kind, you keep that
hand. Those are pat hands that are top of the line. You won’t try to improve any
of them.
You might be tempted, on rare occasions, to break up a straight flush to try
to improve to the royal flush. It’s not worth it.
Here’s Why
With a straight flush, you have a 100% chance of a 50 for 1 payoff. That’s an
expected value of 50 units. If you discard a card trying to hit the royal flush,
you only have a 2% chance of upgrading that payoff to 800 units. An expected
value of 50 is better than an expected value of 16.
The 4 of a kind and the straight flush are the only hands you’ll prefer over
a 4-card draw to a royal flush, though. You’ll prefer a 4-card draw to a royal
flush to every other pat hand in the game.
You’ll never break up any of the other pat hands for a 3-card draw to a royal
flush, though. These include the full house, flush, straight, and 3 of a kind.
The probability of hitting that royal flush when you need 2 more cards is just
too much of a longshot.
But you will prefer 3 cards to a royal flush to 2 pair or a pair of kings.
The even money payoff on those hands barely make them worth holding onto.
In fact, if you have 2 pairs, you’ll discard one of those pairs if you have a
pair of kings or aces. You want to try to get one of those higher value 4 of a
kind hands.
What Is Jacks Or Better In Poker
You’ll notice, too, that we’ve mentioned outside straight draws and inside
straight draws. You might not already know the difference.
An outside straight draw is one where the rank of the card you need is on the
outside of the cards you already have. For example, if you have 10, J, Q, K, you
can fill your straight with a 9 or an ace. That doubles the probability of an
inside straight draw.
Here’s an example of an inside straight draw:
9, 10, Q, K.
Only one card can fill this straight-the jack.
In the first example, you have 8 possible ways of making your hand. In the
second example, you only have 4 possible ways of making your hand.
That’s a big difference.
Where to Find Triple Bonus Poker Online for Free or Real Money
Bonus Poker Free Game
Triple Bonus is actually not one of the more popular video poker offerings
online, but many of the online casinos we recommend offer it in both free and
real money versions. If you’re dead set on playing this VP game and no other,
check the list of games offered at the casino before signing up.
We like to recommend playing for free money just long enough to get a feel
for the game. But gambling is meant to involve risk and reward. Free Triple
Bonus Poker games offer no reward and no risk. They’re great as training tools,
but not for any other reasons, really.
Conclusion
Triple Bonus Poker is a great game for players who like to chase large hands
and get big payoffs. Such players are willing to sacrifice some of the sureness
of a steady return in exchange for the shot at big wins.
If you’re already familiar with Bonus Poker and Double Bonus Poker, you’ll
have little trouble understanding and/or playing Triple Bonus Poker. The
strategies for the variations are all similar.
If you do play Triple Bonus, look for the 10/7/5 or the 10/7/4 pay tables.
Any Triple Bonus Poker game that pays off 9 for 1 for a full house isn’t worth
playing. The payback percentage is just too low.
In 9/6 Jacks, for instance, 'QJ8', 'KQ9' and 'KJ9' are preferred to AKQJ. These are all 3-card straight flushes with two high cards and two gaps. In 8/5 Jacks (whether the quads return 25 or 35), 'QJ8' is preferred to AKQJ, but 'KQ9' and 'KJ9' are not.
The easy part of this, discussed last week, is that the 3-card straight flushes decrease in value by about 20¢ (for the 5-coin dollar player) when flushes pay 5 instead of 6. Since the value of the flush doesn't affect the value of AKQJ, it's no wonder that strategy isn't identical between the games.
The harder question is why is 'QJ8' higher than AKQJ and 'KQ9' lower. Both combinations are 3-card straight flushes with two high cards and two gaps. Why should they have different values?
If the other two cards in the hand were lower than an 8, 'QJ8' and 'KQ9' would have identical values. But when the other two cards are such that the hand includes AKQJ, things change. This is an example of a 'straight penalty'.
When we look at 'QJ8' (and the other two cards are AK), there are four 9s in the deck and four Ts which can be used to get straights. When we look at 'KQ9' (and the other two cards are AJ), there are three Js and four Ts to create straights. The reason we have few cards to make a straight is because we were dealt a J and threw it away.
This straight penalty is worth 7.4¢. Whether this is a major or trivial amount depends on your perspective. To me, every 7.4¢ counts.
Let's look closer at 3-card straight flushes when we go from 9/6 to 8/5. All 2-gap straight flushes (such as 'KT9', 'A35', or '357') change in value by 20.35¢. One-gap straight flushes (such as 'QJ9' or '457') change in value by 19.89¢, and the no-gappers (such as 'JT9' or '345') change by 19.43¢. Does this strike you as strange? Only the value of the flush changed. Why would this affect these straight flush draws differently?
When we draw two cards to any combination in a 52-card deck, there are exactly 1,081 different 2-card combinations we could draw. Drawing to any three spades, for example, there will be exactly 45 out of 1,081 combinations that will give us five spades. These 45 5-spade combinations may include a royal flush, one or more straight flushes and the rest will be regular flushes.
On the combinations we are considering, a royal flush is not possible, so the number of straight flushes and regular flushes must add up to 45. To a 2-gap straight flush (such as '347'), there is exactly one combination that will complete a straight flush (namely '56' in this case), so that means 44 regular flushes are possible. To a 1-gap straight flush (such as 'JT8'), there are exactly two combinations that complete the straight flush (namely 'Q9' and '97' in this case), so that means 43 regular flushes are possible. Starting with a no-gap straight flush (such as '678') there are three combinations to complete the straight flush (namely '45', '59' and '9T'), which means there will be 42 regular flushes.
One extra flush opportunity out of 1,081 chances on a dollar game amounts to 0.46¢ when we change the value of a flush by one unit. This is not a number worth memorizing, but understanding why different 3-card straight flush combinations are affected differently by a change in the value of a flush helps you memorize strategies. The more you understand about video poker, the more strategies 'make sense' rather than are just a jumble of unrelated rules.