Odds Table Poker
Introduction
The house edge is defined as the ratio of the average loss to the initial bet. In some games the beginning wager is not necessarily the ending wager. For example in blackjack, let it ride, and Caribbean stud poker, the player may increase their bet when the odds favor doing so. In these cases the additional money wagered is not figured into the denominator for the purpose of determining the house edge, thus increasing the measure of risk. For games like Ultimate Texas Hold 'Em and Crazy 4 Poker, where there are two required initial wagers, the house edge is based on one of them only. House edge figures are based on optimal or near-optimal player strategy.
The table below shows the house edge of most popular casino games and bets.
For example, the exact mathematical equivalent of decimal odds 30 is fractional odds 29/1. However 29/1 is not used in betting markets, instead 30/1 is used, so that is what appears in this converter. For an explanation of the odds types on this table see decimal, fractional and American odds. Blackjack – House Edge from 1% To many gamblers, Blackjack is the best game to play at casino to.
Casino Game House Edge
| Game | Bet/Rules | House Edge | Standard Deviation |
|---|---|---|---|
| Baccarat | Banker | 1.06% | 0.93 |
| Player | 1.24% | 0.95 | |
| Tie | 14.36% | 2.64 | |
| Big Six | $1 | 11.11% | 0.99 |
| $2 | 16.67% | 1.34 | |
| $5 | 22.22% | 2.02 | |
| $10 | 18.52% | 2.88 | |
| $20 | 22.22% | 3.97 | |
| Joker/Logo | 24.07% | 5.35 | |
| Bonus Six | No insurance | 10.42% | 5.79 |
| With insurance | 23.83% | 6.51 | |
| Blackjacka | Liberal Vegas rules | 0.28% | 1.15 |
| Caribbean Stud Poker | 5.22% | 2.24 | |
| Casino War | Go to war on ties | 2.88% | 1.05 |
| Surrender on ties | 3.70% | 0.94 | |
| Bet on tie | 18.65% | 8.32 | |
| Catch a Wave | 0.50% | d | |
| Craps | Pass/Come | 1.41% | 1.00 |
| Don't pass/don't come | 1.36% | 0.99 | |
| Odds — 4 or 10 | 0.00% | 1.41 | |
| Odds — 5 or 9 | 0.00% | 1.22 | |
| Odds — 6 or 8 | 0.00% | 1.10 | |
| Field (2:1 on 12) | 5.56% | 1.08 | |
| Field (3:1 on 12) | 2.78% | 1.14 | |
| Any craps | 11.11% | 2.51 | |
| Big 6,8 | 9.09% | 1.00 | |
| Hard 4,10 | 11.11% | 2.51 | |
| Hard 6,8 | 9.09% | 2.87 | |
| Place 6,8 | 1.52% | 1.08 | |
| Place 5,9 | 4.00% | 1.18 | |
| Place 4,10 | 6.67% | 1.32 | |
| Place (to lose) 4,10 | 3.03% | 0.69 | |
| 2, 12, & all hard hops | 13.89% | 5.09 | |
| 3, 11, & all easy hops | 11.11% | 3.66 | |
| Any seven | 16.67% | 1.86 | |
| Crazy 4 Poker | Ante | 3.42%* | 3.13* |
| Double Down Stud | 2.67% | 2.97 | |
| Heads Up Hold 'Em | Blind pay table #1 (500-50-10-8-5) | 2.36% | 4.56 |
| Keno | 25%-29% | 1.30-46.04 | |
| Let it Ride | 3.51% | 5.17 | |
| Pai Gowc | 1.50% | 0.75 | |
| Pai Gow Pokerc | 1.46% | 0.75 | |
| Pick ’em Poker | 0% - 10% | 3.87 | |
| Red Dog | Six decks | 2.80% | 1.60 |
| Roulette | Single Zero | 2.70% | e |
| Double Zero | 5.26% | e | |
| Sic-Bo | 2.78%-33.33% | e | |
| Slot Machines | 2%-15%f | 8.74g | |
| Spanish 21 | Dealer hits soft 17 | 0.76% | d |
| Dealer stands on soft 17 | 0.40% | d | |
| Super Fun 21 | 0.94% | d | |
| Three Card Poker | Pairplus | 7.28% | 2.85 |
| Ante & play | 3.37% | 1.64 | |
| Ultimate Texas Hold 'Em | Ante | 2.19% | 4.94 |
| Video Poker | Jacks or Better (Full Pay) | 0.46% | 4.42 |
| Wild Hold ’em Fold ’em | 6.86% | d |
Notes
| a | Liberal Vegas Strip rules: Dealer stands on soft 17, player may double on any two cards, player may double after splitting, resplit aces, late surrender. |
| b | Las Vegas single deck rules are dealer hits on soft 17, player may double on any two cards, player may not double after splitting, one card to split aces, no surrender. |
| c | Assuming player plays the house way, playing one on one against dealer, and half of bets made are as banker. |
| d | Yet to be determined. |
| e | Standard deviation depends on bet made. |
| f | Slot machine range is based on available returns from a major manufacturer |
| g | Slot machine standard deviation based on just one machine. While this can vary, the standard deviation on slot machines are very high. |
Guide to House Edge
The reason that the house edge is relative to the original wager, not the average wager, is that it makes it easier for the player to estimate how much they will lose. For example if a player knows the house edge in blackjack is 0.6% he can assume that for every $10 wager original wager he makes he will lose 6 cents on the average. Most players are not going to know how much their average wager will be in games like blackjack relative to the original wager, thus any statistic based on the average wager would be difficult to apply to real life questions.
The conventional definition can be helpful for players determine how much it will cost them to play, given the information they already know. However the statistic is very biased as a measure of risk. In Caribbean stud poker, for example, the house edge is 5.22%, which is close to that of double zero roulette at 5.26%. However the ratio of average money lost to average money wagered in Caribbean stud is only 2.56%. The player only looking at the house edge may be indifferent between roulette and Caribbean stud poker, based only the house edge. If one wants to compare one game against another I believe it is better to look at the ratio of money lost to money wagered, which would show Caribbean stud poker to be a much better gamble than roulette.
Many other sources do not count ties in the house edge calculation, especially for the Don’t Pass bet in craps and the banker and player bets in baccarat. The rationale is that if a bet isn’t resolved then it should be ignored. I personally opt to include ties although I respect the other definition.
Element of Risk
For purposes of comparing one game to another I would like to propose a different measurement of risk, which I call the 'element of risk.' This measurement is defined as the average loss divided by total money bet. For bets in which the initial bet is always the final bet there would be no difference between this statistic and the house edge. Bets in which there is a difference are listed below.

Odds Table For Poker
Element of Risk
| Game | Bet | House Edge | Element of Risk |
|---|---|---|---|
| Blackjack | Atlantic City rules | 0.43% | 0.38% |
| Bonus 6 | No insurance | 10.42% | 5.41% |
| Bonus 6 | With insurance | 23.83% | 6.42% |
| Caribbean Stud Poker | 5.22% | 2.56% | |
| Casino War | Go to war on ties | 2.88% | 2.68% |
| Crazy 4 Poker | Standard rules | 3.42%* | 1.09% |
| Heads Up Hold 'Em | Pay Table #1 (500-50-10-8-5) | 2.36% | 0.64% |
| Double Down Stud | 2.67% | 2.13% | |
| Let it Ride | 3.51% | 2.85% | |
| Spanish 21 | Dealer hits soft 17 | 0.76% | 0.65% |
| Spanish 21 | Dealer stands on soft 17 | 0.40% | 0.30% |
| Three Card Poker | Ante & play | 3.37% | 2.01% |
| Ultimate Texas Hold 'Em | 2.19%* | 0.53% | |
| Wild Hold ’em Fold ’em | 6.86% | 3.23% |
Standard Deviation
The standard deviation is a measure of how volatile your bankroll will be playing a given game. This statistic is commonly used to calculate the probability that the end result of a session of a defined number of bets will be within certain bounds.
The standard deviation of the final result over n bets is the product of the standard deviation for one bet (see table) and the square root of the number of initial bets made in the session. This assumes that all bets made are of equal size. The probability that the session outcome will be within one standard deviation is 68.26%. The probability that the session outcome will be within two standard deviations is 95.46%. The probability that the session outcome will be within three standard deviations is 99.74%. The following table shows the probability that a session outcome will come within various numbers of standard deviations.
I realize that this explanation may not make much sense to someone who is not well versed in the basics of statistics. If this is the case I would recommend enriching yourself with a good introductory statistics book.
Standard Deviation
| Number | Probability |
|---|---|
| 0.25 | 0.1974 |
| 0.50 | 0.3830 |
| 0.75 | 0.5468 |
| 1.00 | 0.6826 |
| 1.25 | 0.7888 |
| 1.50 | 0.8664 |
| 1.75 | 0.9198 |
| 2.00 | 0.9546 |
| 2.25 | 0.9756 |
| 2.50 | 0.9876 |
| 2.75 | 0.9940 |
| 3.00 | 0.9974 |
| 3.25 | 0.9988 |
| 3.50 | 0.9996 |
| 3.75 | 0.9998 |
Hold
Although I do not mention hold percentages on my site the term is worth defining because it comes up a lot. The hold percentage is the ratio of chips the casino keeps to the total chips sold. This is generally measured over an entire shift. For example if blackjack table x takes in $1000 in the drop box and of the $1000 in chips sold the table keeps $300 of them (players walked away with the other $700) then the game's hold is 30%. If every player loses their entire purchase of chips then the hold will be 100%. It is possible for the hold to exceed 100% if players carry to the table chips purchased at another table. A mathematician alone can not determine the hold because it depends on how long the player will sit at the table and the same money circulates back and forth. There is a lot of confusion between the house edge and hold, especially among casino personnel.
Hands per Hour, House Edge for Comp Purposes
The following table shows the average hands per hour and the house edge for comp purposes various games. The house edge figures are higher than those above, because the above figures assume optimal strategy, and those below reflect player errors and average type of bet made. This table was given to me anonymously by an executive with a major Strip casino and is used for rating players.
Hands per Hour and Average House Edge
| Games | Hands/Hour | House Edge |
|---|---|---|
| Baccarat | 72 | 1.2% |
| Blackjack | 70 | 0.75% |
| Big Six | 10 | 15.53% |
| Craps | 48 | 1.58% |
| Car. Stud | 50 | 1.46% |
| Let It Ride | 52 | 2.4% |
| Mini-Baccarat | 72 | 1.2% |
| Midi-Baccarat | 72 | 1.2% |
| Pai Gow | 30 | 1.65% |
| Pai Pow Poker | 34 | 1.96% |
| Roulette | 38 | 5.26% |
| Single 0 Roulette | 35 | 2.59% |
| Casino War | 65 | 2.87% |
| Spanish 21 | 75 | 2.2% |
| Sic Bo | 45 | 8% |
| 3 Way Action | 70 | 2.2% |
Footnotes
* — House edge based on Ante bet only as opposed to all mandatory wagers (for example the Blind in Ultimate Texas Hold 'Em and the Super Bonus in Crazy 4 Poker.
Translation
A Spanish translation of this page is available at www.eldropbox.com.
Written by: Michael Shackleford
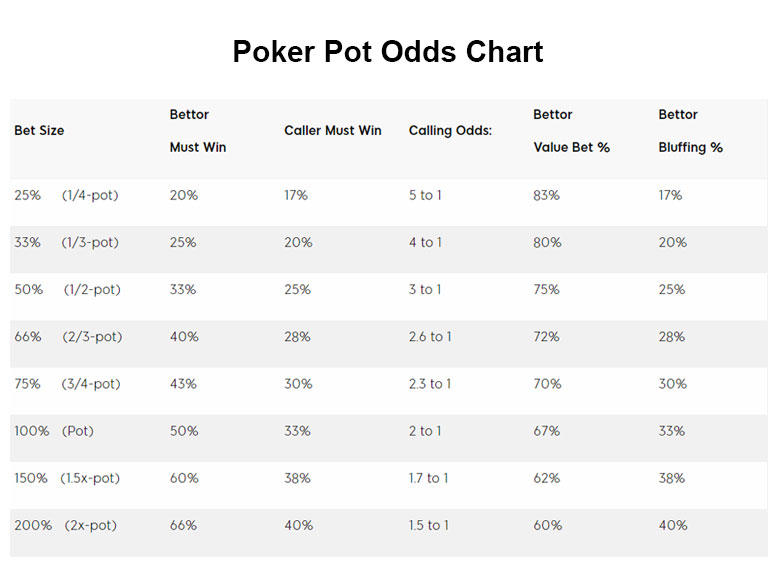
In poker there are good bets and bad bets – the game is simply a way of determining who can tell the difference. This is where the concept of pot odds comes into play. Put simply, pot odds means is there enough in the pot to call a bet.
The fundamental principle of playing a drawing hand in poker is that you need a pot big enough to call. When we have a flush draw or a straight draw we will make our hand on the next card almost 20% of the time (19% for flush and 17% for the straight draw). That is, 20% of the time we will make our desired hand and 80% we won’t. The ratio 20 to 80 can be expressed as odds of 4-to-1. Therefore, if the pot is $80 we can almost call a $20 bet to break-even. I say almost because we have to make a profit so, a call of $20 is appropriate when there is more than $80 in the pot.
Know the Odds
You should already know how to calculate odds based upon the number of “outs”. If you don’t know the odds of hitting certain common draws then please go back and study our previous lesson on calculating odds and outs in poker. For the benefit of this lesson we’ll include the handy chart below:
Table: Odds and outs from the flop and the turn to the river:
We have created a printable PDF version of the poker drawing odds chart (opens in a new window). You will need Adobe Acrobat on your computer to view it on screen. We recommend you print the chart and be sure to memorize these odds, particularly the common draws – as your time is better spent analyzing your opponents’ play rather than attempting to perform mathematical calculations in your head.
Track the Pot Size
Part of the concept of pot odds is to focus on the calculation of how to figure the odds of your hand becoming a winner. The other part of the equation is to know how much is actually in the pot in order to know what odds it is offering you.
If you’re playing poker online then the size of the pot should be in clear view at all times – simple! If you’re playing poker live then it’s as easy as paying attention and using basic arithmetic to know the pot size at every step of the way. All one needs to do is multiply the total amount bet on each street by the number of active players and add that sum to the blinds if they are not participating in the hand. Hold that total in your head and add the subsequent total of the next street’s betting and you will always have the pot total available to calculate your pot odds. Here are some critical words of advice: know what is in the pot at all times. How else can you make proper mathematical decisions?
Calculating the Pot Odds
At this stage you should know the odds of hitting your card(s) and the size of the pot. The next step is to know what odds the pot is offering you. The best way to teach you is to use an example hand. Take a look at figure 1, below:
Figure 1
As you can see, we have 9 outs for the nut flush draw, so the odds of hitting our flush on the river are roughly 20% or 4-to-1 odds. There is $450 in the pot, and player 2 bets $150, which now makes the total pot $600. It’s going to cost us $150 to win $600. How do we calculate these figures to give us the pot odds? This is fairly simple as 600/150 = 4, so we have 4-to-1 odds for our money.
If we want to know the percentage then we add the bet (call amount) to the pot, to give us a total pot figure. In this example it would be: 150 + 600 = 750. Once we have this figure then we would have to perform the following formula: call amount / the total pot size. In our example this would be 150 / 750 = 0.2, or 20%.
Now we know the pot odds, should we call or not? In our example we can justify the call as we’re getting 4-to-1 pot odds and our odds of hitting and winning is also 4-to-1. But remember it’s a break-even call over the long term if we’re only counting the flush draw. Ideally we’d want the pot to be a little bigger or their bet to be a little smaller. However, if we believe that hitting either an Ace of King (giving us 6 additional outs) on the river would beat our opponent then we’d have more than enough odds to call the bet.
In poker, whenever the pot odds exceed the odds against making your hand, it pays to keep playing. When the odds against your hand coming in exceed the reward associated with it, it’s usually a bad deal. A simple way to think about this is as follows:

- When the prize exceeds the cost, you should call.
- If the cost is more than the money you figure to win, fold.
…did you know that AK flops a flush draw 11% of the time?
The new book Optimizing Ace King has a complete chapter on playing draws (along with chapters on playing pairs, turn & river play, and even ideal lines when AK totally misses the board).
As a bonus for being a Pokerology reader, use code POKEROLOGY at checkout to save $5 when you pick up your copy.
Let’s look at another example:
Figure 2
Here we have a straight and a flush draw, meaning we have 15 possible outs. The odds of hitting one of our outs on the turn is 31.9% or 2.13-to-1. The pot contains $36 ($24 + $12) and it’ll cost us $12 to call.
Are we getting enough pot odds to call? Let’s do the figures, first in odds…..$36 (total pot) / $12 (cost to call) = 3. Expressed as a ratio this would be 3-to-1 odds, meaning we’ll win once every 4 times. In percentage terms… the pot odds can be expressed as 25%. Our drawing odds are 31.9%. Since the pot is offering us better odds than our draw, we should call the $12 bet.
Let’s continue with this hand example. As you can see in figure 3, we didn’t hit on the turn, we check and our opponent then bets $60 into the existing $48 in the pot.

Figure 3
Are we still getting the correct pot odds to call in the hopes of hitting a straight or flush? The answer is no.
Poker Hands Odds Table
The pot odds are now 1.8-to-1 (108 / 60) or 35.7% in percentage terms. Our drawing odds are 2.07-to-1 or 32.6%. Since the pot odds are less than the odds of hitting, in this instance we should fold. To call a bet here we’d need the pot to be a little bigger or our opponents bet to be a little lower. He has priced us out with his overbet.
So, that old feeling we had, “There is a bunch of money in the pot, I call”, was and is a sound tactic. Now we know more precisely when it is profitable and when it is not profitable to go in on draws. Knowing pot odds does two things; it lets us concentrate on the other players and turns poker into a game of skill.
Make Your Opponents Pay
Let’s take a quick look at a situation when you’re the one with a made hand and you figure one or more of your opponents to be drawing. Understanding the concept of pot odds should help you to determine an appropriate bet size and charge your adversaries for their possible draws.
Imagine raising a bunch of limpers from late position, holding pocket Jacks. The big blind and the three of the original limpers all call your raise and the five of you watch a flop of :
You’ve hit middle set but there are both straight and flush draws staring at you along with four opponents. There is $86 in the pot and everyone checks to you. You are definitely going to make a continuation bet but you need to decide on how much. Allow me to provide a check list of criteria to think about that as you become more experienced will become so automatic as to not even require any conscious thought.
- Know the pot size – in this case $86.
- Acknowledge the texture of the flop and tendencies of your opponents in terms of potential threats to your holding. Limpers and callers are many times on draws.
- Know the odds to the potential draws the flop offers. In this case both flush and straight draws.
- Make a bet that will not offer the potential draws the correct odds.
- You should bet the size of the pot, $86, in order to make the odds being offered by the pot only 2-to-1 which would not be attractive odds for draws.
If it is true, and I believe it is, that the bulk of your poker profit comes from the mistakes of others rather than you own brilliant play, then identifying opponents that overpay to draw to their hands is critical information. Aside from just playing too many hands, one of the biggest and most expensive mistakes less experienced poker players commit is paying too high a price to try to make their draws. Ferret this information out by tracking the pot and watching showdowns and then you can determine how to manipulate the size of the pot against that opponent in a future hand.
Implied Odds
Poker Odds Table Outs
This is an extension of pot odds and represents the ratio of the total amount you expect to win if you complete your hand, to the amount you would need to call to continue. Put simply, you don’t have the correct odds to call, but if you reason that there’s a good chance that your opponent will bet again when you hit your draw, you might be getting the implied odds to call.
While implied odds are an important tool to be aware of, particularly in no limit hold’em, many less disciplined players abuse it by using it as a justification to chase draws that are not getting the proper pot odds. While pot odds can be calculated with total accuracy, calculating implied odds takes some guess work and knowledge of your opponents’ tendencies. It’s more of an art than a science.
Are your opponents mostly fish?
If yes, they tend to offer a lot of implied odds – but most players leave chips on the table by missing aggression AND using incorrect bet/raise sizes when they hit their hand.
To ensure you don’t fall into the same trap, sign up for CORE today and pay special attention to the lessons on:

· Value Betting (Level 1)
· Overbetting (Level 2: Postflop)
· Range Elasticity (Level 2: Ranges)
Enroll today for just $5 and see how pot odds (along with 100+ other concepts) fit into the entirety of your poker playbook!
Tournament Play
Much of what has been offered so far is beneficial for both cash games and poker tournaments. But you should approach opponents in tournaments that are desperate a little differently. In a cash game, being pot committed doesn’t really come into play. The term pot committed simply refers to a player who has half or more of his chips already in the pot so if he loses this pot he is pretty much finished anyway. This player will be calling, not based upon the pot odds, but due to his predicament. Players calling in tournament play without the correct pot odds does not necessarily indicate poor play. Calling may well still represent their best chance mathematically to move forward in the tournament and make some money. Hence the expression, do or die!
The reverse situation relative to pot odds can also occur in tournament play. Imagine being in a situation wherein you have the correct pot odds to call but folding could be the better option to advance. An example of this type of phenomenon would be holding the nut flush draw with one card to come with two other opponents already all-in by a monster stack late in a poker tournament. The pot could be offering you greater than the odds required to make the call mathematically correct but the fact still remains that you will miss your flush 80% of the time. If you were on the bubble with the big stack bully already having two other players all-in and you knew you would only prevail in the hand 20 percent of time – I think a fold would be in order.
Many believe that pot odds aren’t nearly as important in tournament play. This is especially true in the lower stake “fast” events that are typical in both live and internet play. These players focus on the odds of their opponents’ calling based upon the size of chip stacks. While some of this is true, if you begin to ignore pot odds because you are in a poker tournament, you will begin to slide down a slippery slope. If you are planning to make a decision that is not in accordance with good pot odds play, you should have a very significant reason.
Put in the Work
Knowing what and how to use pot odds is essential if you wish to become a winning poker player. Learning how to use these concepts to your advantage can put you well ahead of a vast legion of players that are just too lazy to put in the work. They are playing on feel and their gut instincts and proud of it. I’m happy they’re proud of this approach because I know they can’t be proud of their bankrolls. These “proud” players are the assets you need in both cash games and tournaments. Let them be proud – you should put in the work – you’ll be glad you did as you’ll end up with their bankrolls.
Related Lessons
By Tom 'TIME' Leonard
Tom has been writing about poker since 1994 and has played across the USA for over 40 years, playing every game in almost every card room in Atlantic City, California and Las Vegas.